Introduction
This assignment is very similar, but not identical, to one used in CS-343 last semester, and this web page is derived from the corresponding page from last semester. If you find a discrepancy between this web page and how we did the design in class, it’s probably a mistake: do it the way we did in class. Also, there is some material from last semester’s assignment in this web page that you already know from Assignment 3; it is here because it might help as you review Assignment 3 for the exam on March 2.
Although this assignment is not due until March 4, material from this assignment will be tested during the exam on March 2.
For this assignment, you are to implement a 4-bit version of the MIPS ALU developed in Appendix C of the textbook. The DE1 logic kits could easily handle a full 32-bit implementation, except that the limited number of switches, keys lights would make it difficult to test such a device easily.
The Assignment
-
Set up the project
Create a directory named Assignment 4 under your My Projects directory.
Copy hex2sevenseg.v and the full adder schematic(s) and symbol file(s) from Assignment_03 into your Assignment 4 directory.
Use the New Project wizard to set up the project just as you did for the previous two assignments. Use 4_bit_mips_alu (or something similar) as the project name, and name the top-level design entity Assignment_04_Testbed. When the wizard asks if you want to add files to the project, say “yes,” as you did for Assignment 3.
-
Create a symbol for hex2sevenseg.v
(You should already be familiar with this material from Assignment 3, but it may be useful for review purposes.) Seven segment displays are ubiquitous, so you are familiar with them even if you didn’t know that was what they are called. The DE1 has four of them, and we are going to use all four of them for this assignment. Each display digit can show any of sixteen characters by lighting up different combinations of the seven segments:
_ _ _ _ _ _ _ _ _ _ _ _ | | | _| _| |_| |_ |_ | |_| |_| |_| |_ | _| |_ |_ |_| | |_ _| | _| |_| | |_| | | | |_| |_ |_| |_ |
These sixteen characters, of course, are a perfect match for displaying hexadecimal digits. The Verilog module I am supplying accepts a 4-bit binary number as its input, and outputs the correct settings for the seven segments to display the corresponding hexadecimal digit.
Open hex2sevenseg.v in Quartus, and create a symbol for it, just as if it was a block diagram file. This will cause the code to be compiled: make sure there are no mistakes in the process. The symbol will have a four-wire input named Hex[3..0], and a seven-wire output named Segments[6..0]. The conventional way to name the segments of a seven-segment display is with the letters A—G (or a—g), like this:
A F B G E C D
The Segments subscripts 0—6 correspond to segment letters A—G, in that order.
-
Create a symbol for your full-adder
You already went through this in Assignment 3, and do not need to do anything if you copied the symbol file(s) as well as the schematic file(s) over from Assignment 3.
-
Create one slice of the ALU.
Create a new block diagram file for one bit-slice of the ALU. There will be eight separate (individual) input pins for A, B, Cin, SLTin, Ainv, Bneg, f[1], and f[0]. There will be three output pins: Result, Cout, and SLTout.
The bit slice module is fully designed in the textbook. You can simplify the Quartus implementation in a few ways.
First, you can use the Altera lpm_mux megafunction to implement the 4×1 multiplexer used for selecting the output of the bit slice. The alternative would be to assemble all the AND, OR, and NOT gates to build the MUX. (But you do need to be able to draw the gates to implement a multiplexer on the exam.)
Use the symbol tool to open the Altera library, open up the “megafunctions” folder, and select the lpm_mux megafunction. You do not need the “repeat insert” option, but you do want the “launch wizard” option. Tell the wizard you want a mux with four data inputs and one data output, and it will generate all the files needed for the multiplexer and a symbol you can insert into your bit slice module.
You will probably find it convenient to right-click on the symbol and flip it vertically, making the data inputs line up better with the AND, OR, full-adder, and SLT elements of the schematic.
The SLTin input pin goes to input #3 of the 4×1 multiplexer. The SLTout output pin connects directly to the Sum output of the full adder, which also goes to input #2 of the 4×1 mux.
The textbook uses 2×1 multiplexers to select whether the A and/or B inputs should be inverted or not before going to the AND, OR, and full adder. Rather than build the multiplexers (or use another lpm_mux megafunction), you might find it easier just to use an XOR gate as shown in class. For example, A' = A ⊕ Ainv will make A' the same as A if Ainv is 0, but will make it the opposite of A if Ainv is 1.
Name this diagram “bit_slice”, save it as a symbol.
-
Build the ALU schematic.
Create a new schematic for the ALU with input pins for the 4-bit values of A, B, and the function code (function_code), and output pins for the 4-bit result (ALUout) and condition code (condition_code).
Insert four bit_slice symbols; they will each get names that appear in the lower-left corner of the symbol, names like “inst_3”; rename them “slice_3”, “slice_2”, “slice_2”, and “slice_0” by double-clicking on the instance names and typing over them. I suggest you lay out the slices vertically with slice_3 on top, but this is not a requirement.
Here is a description of what you have to do to complete the ALU schematic. This screenshot of the top part of the schematic should help make some of the points clear. Right-click and select “view image” to see a clearer copy.
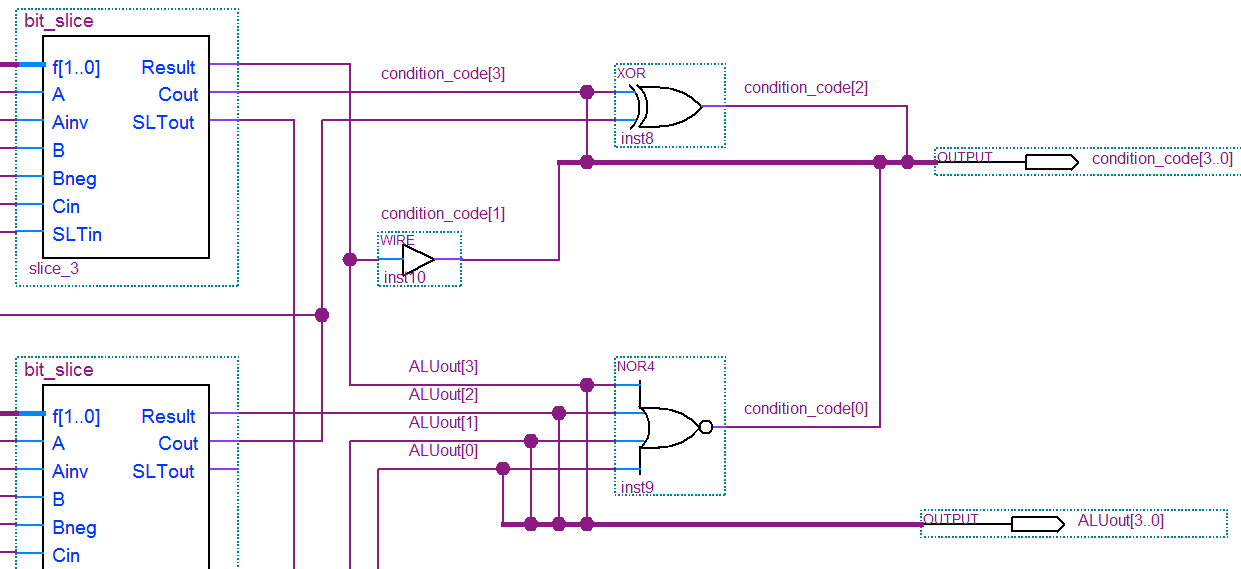
-
Connect the Cout of each slice to the Cin of the next slice. As shown in the screenshot above, Cout of slice 3 is the “Carry” condition code bit, and gets connected to pin, condition_code[3].
Remember, Cin of slice 0 connects to the Bneg input pin.
-
SLTin for slices 1—3 are connected to logic 0. Look under the
“other” folder of the primitives in the Symbol Tool, and locate the symbol for ground (gnd),
which is equivalent to the logic 0 value. You can put in one ground symbol and connect it to all three
slices. If you prefer, you can put in three separate instances, one for each slice.
Connect SLTout of slice 3 to SLTin of slice 0. The SLTout from slices 0—2 do not connect to anything.
In the figure, you can see the wire leaving SLTout from slice 3 on its way down to SLTin of slice 0, and you can see that SLTout from slice 2 doesn’t go anywhere.
-
The A and B input pins get connected to the A and B inputs of the slices. You can pull out Bus Lines
from the A and B pin arrays, and connect node lines (wires) from each slice to the bus lines.
Right-click on the node line, and select the bottom menu item (Properties) to name the node lines so the
subscripts match the slice numbers.
The four function inputs connect to the Ainv, Bneg, f[1], and f[0] inputs of all four slices. Ainv connects to function_code[3], Bneg connects to function_code[2], f[1] connects to function_code[1], and f[0] connects to function_code[0].
Don’t forget that function_code[2], connects to the Bneg) inputs to all the slices and to the Cin input to slice 0.
-
Condition code bits condition_code[2..0] correspond to “oVerflow,”, “Negative,”, and “Zero” respectively.
The Negative condition code bit (condition_code[1]) is true whenever the leftmost bit of the result is 1. So condition_code[1] is really the same as Result[3]. But you cannot use two different names for the same node line in Quartus. To solve this problem, insert a “wire” symbol that does nothing logically, but breaks a node line into two parts that can be given different names. The wire comes from the “buffer” folder of the Symbol Tool. You can see the wire symbol (it looks like an inverter without a bubble on the output) in the figure above.
The Zero condition code bit (condition_code[0] is true whenever all four result bits are 0. The 4-input NOR gate on the right side of the figure takes care of this.
Create a symbol for your ALU to use in the top-level module.
-
-
Create the top-level module, Assignment_04_Testbed
Create a new block diagram to use as the testbed for the assignment. There will be four input pins for connecting switches 7–4 to the four bits of operand A, four input pins for connecting switches 3–0 to the four bits of operand B, and four input pins for connecting key inputs (blue pushbuttons) 3–0 to the four function code bits.
Use seven output pins for the segments of Hex_0, the seven segment display to be used to show the ALU result; seven pins for Hex_1, which will be used to display the condition code outputs; seven pins for Hex_2, which will be used to display the value of the B operand; and seven pins for Hex_3, which will be used to display the value of the A operand.
Add an array of eight output pins to connect to Red LEDs 7–0 to show the states of the switches, and an array of four output pins to connect to Green LEDs 3–0 to show the states of the four pushbuttons.
Insert four copies of the hex2sevenseg symbol, and connect the outputs to the pin arrays for Hex_0, Hex_1, Hex_2, and Hex_3.
Using the pushbuttons for the function code bits is nice: when testing, you will be able to set up two operands using the slide switches for A and B, and then easily test different function codes by manipulating the pushbuttons. But there is a problem: the pushbuttons generate a logic 0 when they are pressed, and logic 1 when they are not pressed, just the opposite of what you would think they would do. (Somebody saved a transister somewhere doing it this way.) So you need to invert each Key input before connecting it to the function_code inputs of the ALU.
You could use four inverters to invert the four Key inputs, but if you use a bus for the inputs, you can use a Quartus megafunction to add all four inverters as a single symbol. It’s called lpm_inv in the megafunction library. Setting it up is even easier than the 4×2 mux you set up earlier. The result looks like this:
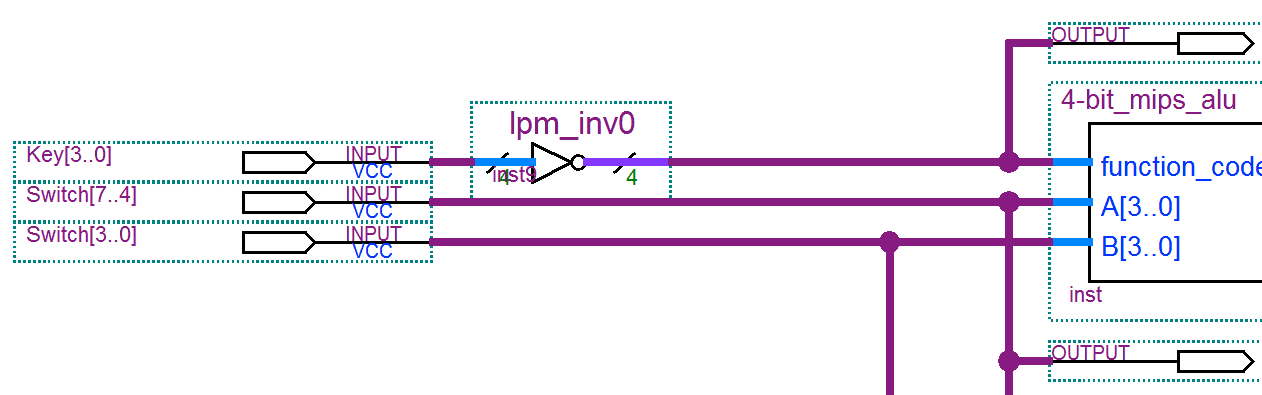
Run Analysis & Synthesis, ignore all the warnings, and go to the Pin Planner, where you should find all the input and output pins listed. Use the DE1 I/O Pins web page, and make the pin assignments. There are 52 pin assignments to make: what fun!
-
Build and Debug
Compile the project. There must be no error messages and only the two warnings about “output load capacitance” and nused “Reserve All Pins.”
If you get any errors and/or any warnings other than those two, fix the problems before proceeding.
-
Test and Debug
Once you can build the project cleanly (like getting rid of syntax errors in software), it’s time for systematic testing to make sure the design actually works as intended (like getting rid of semantic errors in software).
Testing the project is a critical component of the assignment. Paradoxically, perhaps, you might learn more if you do have semantic errors to correct: by reasoning about what causes wrong behavior, you can get a better sense of how the ALU works. On the other hand, semantic errors can be hard to locate and fix, so let’s hope your testing goes smoothly.
-
Start with all the slide switches off and the four keys not pressed. The four hexadecimal displays
should show 0010.
The left two digits are zeros are because all the slide switches are off. The 1 (00012) indicates Carry, oVerflow, and Negative are all false (zero); but the Zero bit is true (one). The right zero is the result, which is indeed zero. The result is zero because the function is 00002 (no keys are pressed), which says not to invert A, not to negate B, and to select the top input to the 4×1 multiplexers in the bit slices, which gives the AND the two operands: 0000 & 0000 => 0000.
If the display is something other than 0010, you need to determine whether the problem is in how the A and B operands are being passed to the seven segment displays (the problem is in the testbed); how the condition code bits are being computed (probably a problem in the ALU module where the condition code bits are generated), or in the design of the bit slice (how the A and B bits get ANDed together and how the output of the AND gate goes from input number 0 of the 4×1 mux to the result output of the slice).
-
One by one, starting at the right end, slide each slide switch into the on position. The hex displays
should show the values 0010, 0110, 0310, 0710, 0F10, 1F81, 3F83, 7F87, and FFAF in that sequence.
As you slide switches 0—3 up, you are generating the binary values 1, 3, 7, and 15 for the B operand; the second hex digit shows those values. So far, the condition code and result values don’t change because the A operand is still all zeros, and ANDing anything with zero is always zero.
As you slide switches 4—7 up, the left hex digit shows the binary values 1, 3, 7, and 15 for the A operand. Because the B operand is all ones at this point, the result matches the value of the A operand. That is, the left digit and right digit are the same. (1 & X => X).
For A operand values 1, 3, and 7, the condition code value is hex 8 (10002). The value of the Z bit (on the right) is off because the result is no longer zero. The C bit is also set, which is an artifact: even though the output of the full adders is not being output as the result, the sum of the two operands is still being computed, and adding any of these values to 15 produces a carry out of the leftmost full adder, which shows up as the C bit of the condition code being 1.
When the A operand is 15, the condition code changes to hex A (10102). There is still a carry out of the leftmost full adder. But in addition, the N bit is set, indicating that the result (11112) is a negative value.
-
Slide all the switches off, and press the two leftmost pushbuttons (Key 3 and Key 2). The display should
change from 0010 to 00AF. Check the green LEDs to make sure the pushbuttons are actually working; they
can be sticky sometimes.
Key 3 inverts the value of the A operand, (0000 => 1111), and Key 2 does the same to the value of the B operand (with the added feature that C0 is also set to 1). So the full adders are computing 1111+1111+1 => 1110 with a carry out from the leftmost full adder, which shows up as the C bit of the condition code. But the result displayed is the output of the AND gates: 11112. There was no overflow, but the result is a negative value, and is not zero.
Note that the C and V condition code bits are logically irrelevant when performing AND, OR and SLT functions. But they are generated anyway, and looking at their values can help verify that the circuit is working correctly.
- Verify that the OR operation is working correctly by pressing Key 0 and entering various values for the A and B operands. For example 4 | 1 => 5; C | A => E, etc.
- Verify that the Add operation is correctly by pressing Key 1 for different combinations of A and B operands. Add two positive values that do not overflow: 3 + 4 => 7 with C, V, N, and Z all zero. Add two positive values that do overflow: 5 + 5 => A (which is the two’s complement representation of negative 6). The condition code bits should be 6 (V and N) because there was overflow and the result (which “should” be positive) appears to be negative. Perform similar experiments with negative operands that do and do not overflow.
-
Check subtraction. Press Keys 2 (Bneg) and 1 (select the full
adder outputs from the 4×1 muxes).
0090 0 - 0 is calculated as 0 + F + 1, so the the C bit is set because the carry in on the right propagates all the way across to the carry out on the left. The Z bit is set because the result is zero. 0F01 0 minus -1 is calculated as 0 + 0 + 1 = +1, with no carry, no overflow, not negative, and not zero. 786F 7 minus -8 is calculated as 7 + 7 + 1 = F (which is -1, not the 15, the “correct” answer. There is no carry out the left end, but there is overflow (there is a carry into the leftmost bit, but not a carry out), the result appears to be negative, so the N bit is set, and the result is not zero, so the Z bit is not set. 6E68 6 minus -2 is calculated as 6 + D + 1 = 8. This is wrong; the answer should be +8, but that value cannot be represented in four bits. The V and N bits are set because the result is wrong and appears to be negative (8 is the two’s complement representation of -8). - Check the SLT function. With everything above working correctly, you can check the SLT function without worrying about the condition code settings, just the result. The result should be hex 0 (00002) any time the value of operand A is not less than the value of operand B. And it should be 1 (00012) whenever the value of operand A is less than operand B. Perform the SLT function by pressing Keys 0, 1. and 1. (Keys 0 and 1 combine to select the bottom output of the 4×1 mux in the slices; Key 2 causes the B operand to be negated so the full adders compute A-B.) Here are some of the display values you should see: 5590 (5 is equal to 5, not less than it); 5601 (5 is less than 6) F081 (hex F is -1, which is less than 0); F890 (-1 is not less than -8).
-
Start with all the slide switches off and the four keys not pressed. The four hexadecimal displays
should show 0010.
Submit The Assignment
- Once you have tested that your ALU works as specified, simply log out of your account so that your project will be copied back to oak, where I will go to get a copy for grading. Send me an email message when your assignment is ready.
- Be sure to put your name in your email message!
-
Do not submit the assignment until you have actually tested it to be sure it works. If you tested it but cannot get it to work correctly, you may submit the assignment for partial credit, provided you tell me in your email what problem(s) you observed during testing.
- The Subject line must be CS-343 Assignment 4 to avoid my spam filters.
- Send your email to vickeryATbabbage.cs.qc.cuny.edu.
See the course syllabus for grading and late homework policies.